この記事ではナイキスト線図とナイキストの安定判別法についてまとめます。一巡伝達関数(開ループ伝達関数)が安定であったとしても、フィードバック後の閉ループシステムが安定とは限りません。ナイキストの安定判別法は、閉ループ極の計算をせずに図的に安定性を判別する方法です。ここでは、ナイキストの安定判別法について説明を行う。
一巡伝達関数と閉ループ制御系
ここでは、閉ループ系の安定性について確認します。まず、および
が与えられているものとします。
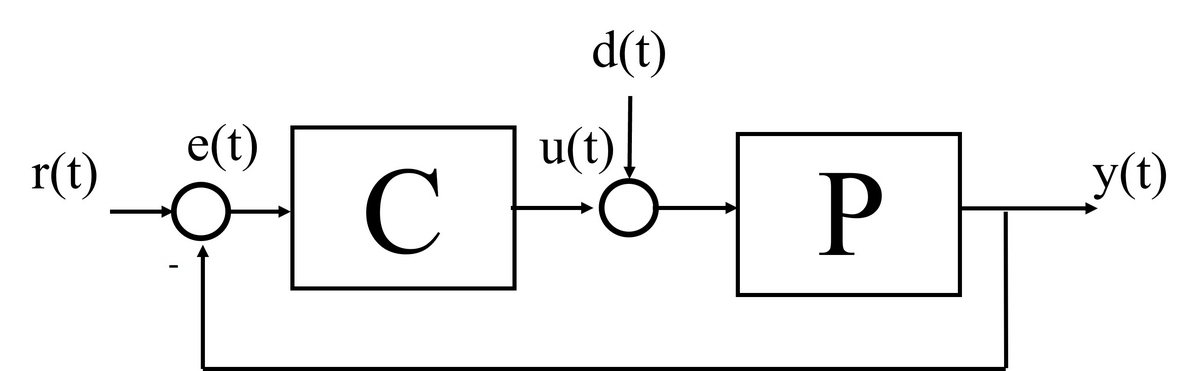
ここで、
\begin{equation} L(s) = P(s) C(s)\end{equation}
を一巡伝達関数と呼びます。閉ループ系の入出力特性は次のように与えられます。
\begin{equation} \frac{y}{r} = \frac{P(s)C(s)}{1+P(s)C(s)}\end{equation}
\begin{equation} \frac{y}{d} = \frac{P(s)}{1+P(s)C(s)}\end{equation}
閉ループ系の安定性を一巡伝達関数の不安定極の数と周波数応答データによって導きます。角周波数
が
から
の範囲で動いたとき、
の軌跡をナイキスト軌跡と呼びます。
ここでは、仮定として,
の間に不安定な極零相殺が無いものとします。安定判別法は以下の通りです。
安定性判別法
- 一巡伝達関数が極零相殺はないものと仮定する。
- ナイキスト軌跡
,
を描く。
- ナイキスト軌跡が点(-1+0j)の周りを時計回りに回る回数を
とする。
- 一巡伝達関数の極のうち、実部が正となる極の数を
とする。
の値が零であれば閉ループ系は安定であり、そうでなければ不安定である。
一巡伝達関数が安定な場合
まずは、一巡伝達関数が安定な場合について周波数応答データ
を複素平面上にプロットします。このとき、ナイキスト軌跡が点(-1+0j)の周りを時計回りに回る回数が零であれば安定です。
一巡伝達関数として
\begin{equation} L(s) = \frac{K}{(s+1)^3}\end{equation}
を与えます。
ここで、のとき、-1を周回する回数は図から零回であることがわかります。
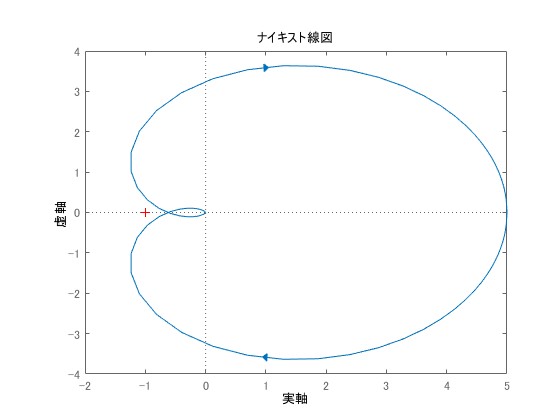
赤色の点を周回していません。の場合について、閉ループ系を組んでステップ応答を表示したものが以下の図です。
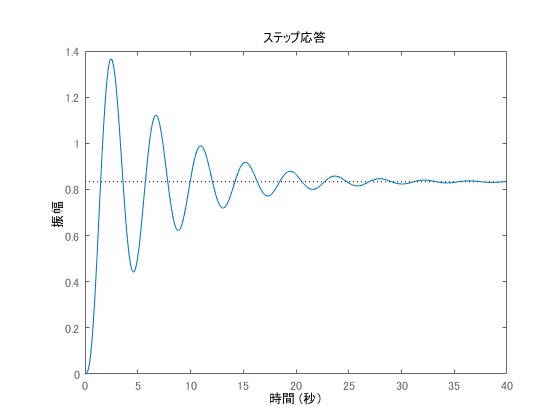
安定であることが応答から確認できます。他方、上記のナイキスト線図がであることから、
とした場合に赤の点(-1)を周回することが容易に予想できます。実際、
としてナイキスト線図を導出すると次のようになります。

このとき、同様に閉ループ系のステップ応答を導出すると次のようになります。ナイキストの安定判別法から上述の結果により不安定であることがわかりましたが、実際に応答が発散していることが確認できます。

一巡伝達関数が不安定な場合
一巡伝達関数が不安定な場合として
\begin{equation} L(s) = K\frac{(s+3)^2}{(s-1)(s+1)^2} \end{equation}
を考えます。このとき、となります。
のときのナイキスト線図を示すと次のようになります。

時計回りに回る回数はとなります。そのため、
が成り立ちます。実際、閉ループ系のステップ応答は次のようになります。

系が安定となっていることが確認できます。ここで、とすると次のナイキスト線図を得ます。

-1を時計回りに周回するためとなり、不安定となります。この場合の閉ループ系の不安定極の数は2です。実際、応答波形は発散します。
閉ループ極を計算すると -1.6090 + 0.0000i、0.0545 + 1.4739i、0.0545 - 1.4739iであり、不安定極の数が2であることが確認できます。

PID制御との関係
PID制御では、に極を持つが、正の零点ではないため上記のカウントはしません。制御対象が安定であれば
として扱うことになります。
スモールゲイン定理との関係
制御対象および制御器が安定な場合には、の大きさが任意の
について1未満であれま-1を回ることはないため、閉ループ系の安定性が補償されます。
以上がナイキストの安定判別法に関する関連記事になります。本記事は以上です。