この記事では状態方程式に基づく制御について1つの記事にまとめます。状態フィードバック制御の個々のトピックの詳細を説明した記事へのリンクは都度貼っています。
- 状態方程式の基本事項
- 可制御性と可観測性
- 同値変換による状態座標の変更
- 極配置による状態フィードバック制御
- 最適レギュレータによる状態フィードバック制御
- 状態オブザーバと併合系による制御
- 実機実験とシミュレーション
- 状態空間モデルの応用(Mamba)
- 制御工学チャンネル内の状態フィードバック制御関連ページ
状態方程式の基本事項
状態フィードバック制御は、制御工学において最も基礎的な制御手法の一つです。その実装にはまずモデル化が必要になってきます。ここでまず状態方程式の主な記号について説明していきます。

tは時間であり、応答を表すグラフの横軸で用いることになります。xは状態ベクトル、uは制御入力、yは制御出力です。
状態方程式では状態ベクトルを使ってシステムのダイナミクスを表現します。n がシステムのは次数であり、この次数が状態ベクトルの要素数に対応します。また A,B,Cはそれぞれ行列とベクトルであり Aは n次の正方行列です。
Bは入力が1個の場合は n次 の縦ベクトル、入力が複数の場合は行列形式になります。Cは出力が一つの場合はn 次の横ベクトル複数の出力がある場合は行列になります。
そして状態方程式は左辺に状態ベクトルの微分、右辺にAx+Buという以下の形で表現されます。
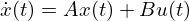
図ではn が3の例も示しています 。n が3の場合には、状態の要素数は3つになり、 A 行列は3×3の行列(ここでは可制御正準形)、B と C はそれぞれベクトル形式になります。状態ベクトルが縦長のベクトルなのでその微分値も縦長のベクトルになります。(以下は n = 3の例)
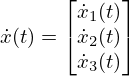
なお、本記事では連続時間状態方程式について説明していますが、離散時間の状態方程式もあり、以下の形式で記述されます。
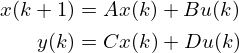
上記で説明した内容は、線形時不変系の状態方程式表現ですが、その他の分類やモデル化の手法、具体例については次のリンク内で詳細を述べています。また、関連動画リンクも以下の記事内にあります。
可制御性と可観測性
可制御性
まず可制御から説明をします。可制御性は、入力によって自由に状態を動かせるかを表現する指標であり、制御工学分野の重要事項の一つです。まず、可制御か可安定であれば状態フィードバックで安定が可能です。例えば、制御対象に対して、u=- Kx という状態フィードバック制御を施す場合、これによって

で与えられる自律システムが得られます。この A-BKの固有値の実部が負であれば自律システムは安定になります。もし、システムが可制御もしくは可安定であるならば、そのようなことを実現するKが存在するといえます。
ここで可制御であれば可安定であるというのは成り立ちますが、逆に可安定であっても
場合によっては可制御にならないようなケースがあります。
例えばもともとAが安定で、Bが零ベクトルというケースでは、Kを適当に与えてもシステムの安定性は保たれますが可制御ではなく、極を任意に配置するといったこともできません。
可制御であれば、適切なフィードバックゲインKを与えることで(A-BK)の極を任意に配置することができます。

図に示すように、ここで可制御性を調べるためには、可制御性行列Uc というものを用います。この行列UcはB、AB、…と並べた行列になっています。仮にこの行列のランクがnであれば、このシステムは可制御になります。
次数ごとの可制御性行列
まず、n = 1 の場合は状態数 1 であり、Ucは次の形になります。
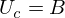
このとき、Bが非零であれば n = 1のシステムは可制御となります。
次に、n = 2 の場合を示します。状態数は2であり、Ucは次の形になります。
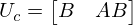
入力数が1の場合は、行列サイズが n × nになります。そのランクが n であれば可制御で、そうでなければ不可制御です。
可観測性
次に可観測について説明します。可観測もしくは可検出であれば制御対象の全状態を状態オブザーバーによって推定することが可能です。ここで先ほどの可制御の場合と同様に可観測であれば、可検出であるという性質が成り立ちます。その逆に可検出であっても必ずしも可観測は成り立たないといえます。

ここで可観測性を調べるためには、可観測性行列を調べれば良いです。この可観測
行列は C,CA…と縦に並べた行列になります。
次数ごとの可観測性行列
まず、n = 1 の場合は状態数 1 であり、Uoは次の形になります。

このとき、Cが非零であれば可観測になります。
次に、n = 2 の場合です。状態数は2であり、Uoは次の形になります。
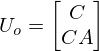
この行列のランクがnであれば可観測であり、 n 未満であれば不可観測となります。ここでは示しませんが、可制御なシステムで可制御正準形があるように、可観測なシステムでは可観測正準形があります。
可制御性・可観測性の具体例や高次の場合のUc, Uoの例については以下の記事内で説明をしています。また、関連動画リンクも以下の記事内にあります。
同値変換による状態座標の変更
ここでは同値変換として説明を進めます。

ここで、図において、行列Tは正則な行列であり、逆行列を持つものを与えます。このとき、行列 T を用いることで、状態の座標の取り方を変えるということになります。これによって同じ入出力特性を満足するような、別の状態 \tilde x に関する状態方程式を、同値変換で得ることができます。
同値変換の前後で保存される性質
この同値変換の前後で、以下の性質が保存されます。
まず、一つ目ですが、入出力特性が保存される変換であるため、両者を伝達関数に変換したものがそれぞれで一致します。
2番目の極については、伝達関数が一致することからも明らかですが、両者の極が一致しており、行列Aと行列 \tilde Aの固有値が完全に一致します。
3番目は、同値変換前のシステムが可制御なら同値変換後も可制御、同値変換前が不可制御なら同値変換後も不可制御と性質が保存されます。

状態方程式の同値変換手順
そして同値変換の手順を説明します。下図で、同値変換の流れを示しています。

まず最初に状態方程式が与えられた時、状態変換

と与えます。このとき、Tの逆行列を使って以下も成り立ちます。

ここで、式を両辺を時間で微分すると

が得られます。
これを踏まえてステップに移ります。
元の状態方程式に、上述の2式を代入すると、ステップ1に記載した式が得られます。そして、ステップ1で得られた式に、両辺の左側からTの逆行列をかけることによってステップ2を得ます。そして
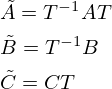
とすることで同値変換が完了します。なお、直流成分(直達項)がある場合は変換の前後でDは変わりません。具体的な同値変換によるメリットについては以下の記事で解説しています。また、関連動画リンクも以下の記事内にあります。
極配置による状態フィードバック制御
状態フィードバック制御は、図に示すように状態量に係数を掛けて、それを制御入力として制御する手法(制御則)になります。制御工学における基礎的な制御系設計理論の一つです。

状態フィードバック制御と自律系
状態方程式として与えられるシステムに入力uを- Kx と与えることによって、以下の自律系が得られます。
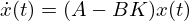
ここで状態フィードバックを施したシステムのダイナミクスは、この行列 A-BK
によって決まります。
なお、制御則において、u = -Kx でなく、u = Kx という表現や u = Fx という表現など、フィードバックゲインおよび制御則の表現形式が色々ありますが、ここでは u = -Kx として進めます。
例えば、n = 3の場合は K は次のベクトル形式になります。

また、仮に同じ n = 3であっても、入力数が 2 の場合は K は次の行列形式となります。

配置された極と制御性能
極配置について説明する前に、まず極についての説明を行います。行列A-BKの固有値がフィードバック系の極であり、次の特性方程式

の根でもあります。フィードバックゲインKを定めると、それによって極の値がいろいろ変化します。
特選方程式の根、制御系の極、それぞれ等しいですので、制御系の極を自由に、いろいろといじることができます。

このフィードバックゲインKの決定により、A-BKの極を適切な場所に配置する、と
いうのが極配置においては重要になってきます。
行列の固有値が極ということから、この極の数は全部で n 個あります。また、全ての極が複素平面の左側にあれば漸近安定であり、これはゲインKを設定する上での必要最低限の条件になります。
スカラシステムの極と応答
スカラシステム(n = 1)の場合、A, B, Kともにスカラ値となります。極は(A-BK)です。自律系は
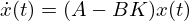
であり、その解軌道は
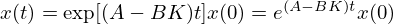
で与えられます。A-BKの値が負であれば t の増加と共に x の値はゼロに収束していきます(安定)。他方、正の値であれば発散します(不安定)。
極と安定性
スカラシステムの場合と同様に、n > 1でも、極の実部が負であれば零に漸近し、一つでも実部が正の極があれば発散します。システムが安定であるためには、全てのが極が複素平面の左側にある、というのが必要な条件になってきます。
それでは例題を見ていきましょう。ここでは n =3すなわち3次のシステムの例を示します。
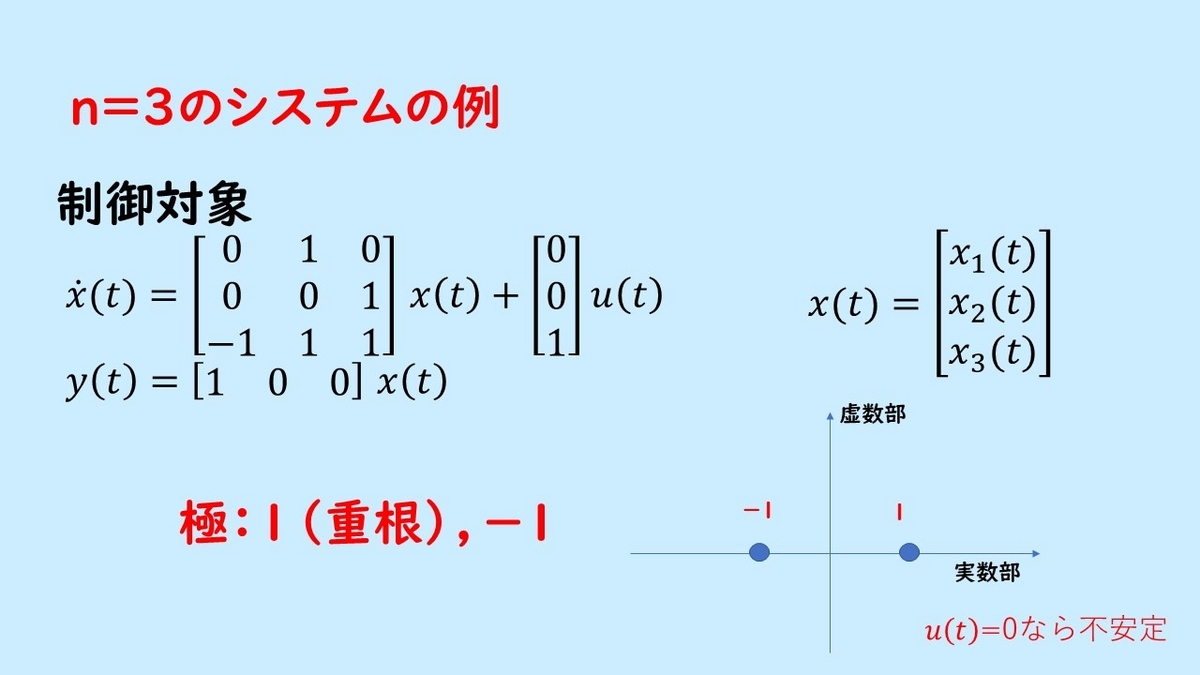
この制御対象は状態数が3個あり、システムの極である a 行列の固有値は1(重根)と-1となります。全ての極が左平面にはないので、仮にこの入力uを 0 とした場合にはこのシステムの状態が発散します。すなわち不安定システムになります。
次に状態フィードバック

を与えることで、極を-1-2-3とすることができます。この結果、元のシステムが不安定であっても、極配置により安定化ができます。

極配置と制御性能
次に極の配置によって、どのような挙動の違いが出てくるかについて説明します。まず以下の図において、ゲイン2は極を虚軸寄り、この左半平面にはあるものの、虚軸寄りに配置して-0.5 -1 -2と配置したケースです。そして、極をより左側に配置して、-5 -6 -7としたものがゲイン3になります。そして、その極配置を実現するためのフィードバックゲインKはそれぞれ異なっています。

このとき、ゲイン3の極をより左側に配置した方が、早く原点に収束し、ゲイン2よりも早い応答を実現することができます。シミュレーションは、下部の動画から確認できます。
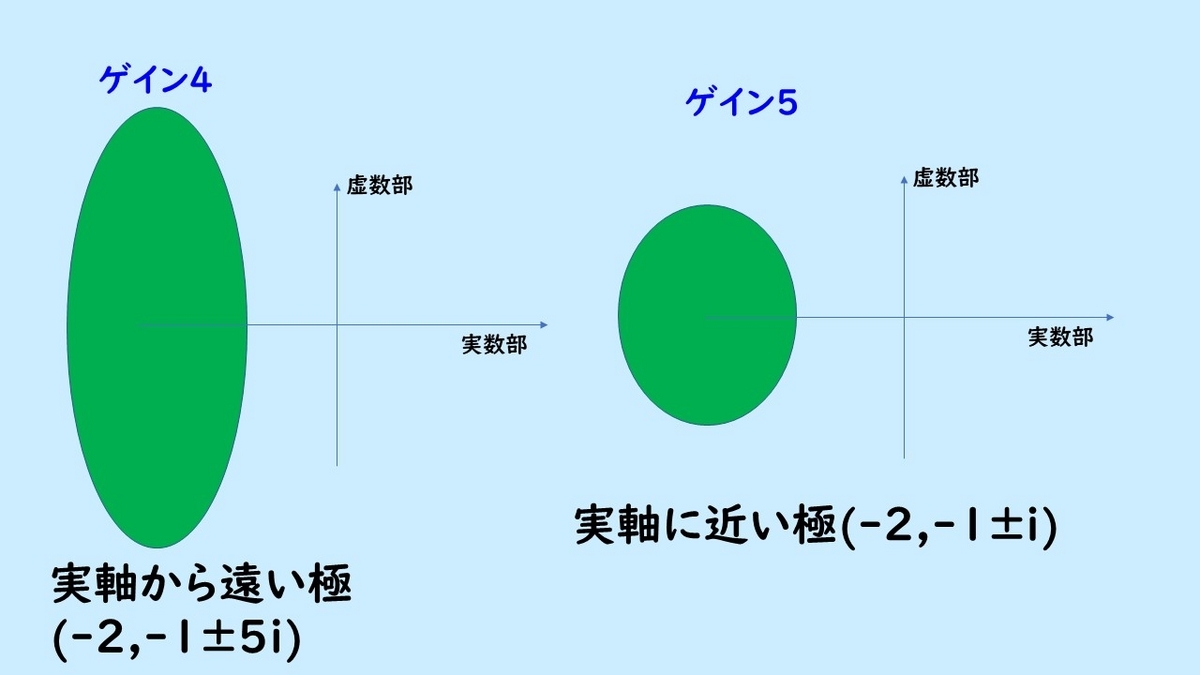
次にゲイン4とゲイン5で実軸から遠い位置に配置した極と、近い位置に配置した極の比較を行います。
実軸から離した-2, -1± 5i に極を配置した場合は振動的な応答波形になります。次に実軸に近い位置に配置した場合、その場合には振動が少ないです。
可制御正準形の極配置
それでは可制御正準系に対する極配置について説明していきます。制御対象が状態方程式表現された場合について、指定の極となるよう状態フィードバックゲインKを求める問題を考えます。このような問題を極配置問題と呼びます。
ここで制御入力uは、状態に比例係数をかけた形で

と与えられます。これによって制御出力を定めます。ここでは、制御対象が可制御であると仮定します。可制御の場合は可制御正準形に変換することができます。
可制御正準形の制御則と構造
それでは可制御正準系について見ていきます。2次の場合の可制御正準系の構造はこのようになっています。
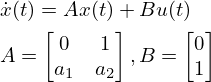
可制御正準系が与えられた場合、制御則u = -Kxを施した特性方程式は次のように与えられます。
2次の場合の特性方程式
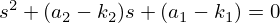
特性方程式の根が理想的な値になるように、係数Kを求めるだけでフィードバックゲインが得られます。例えば、制御対象が2次で、特性根(極)を-2, -1の二つに設定したい場合、理想的な特性方程式は
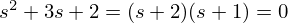
であり、これと係数が合うようにk1とk2を定めればフィードバックゲインが得られます。また、複素数を配置したい場合(-2±i)であれば
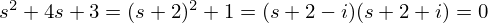
に合わせて係数4, 3に対応してk1,k2を定めれば極配置できます。このように、極配置により制御システムの特性を決定できるます。可制御でなければ一部の極については所望の配置ができないことに注意する必要があります。
以下の記事では3次システムの例や動画リンクなどを置いています。
最適レギュレータによる状態フィードバック制御
極配置と共に、状態フィードバックゲイン設計で有用な手法として最適レギュレータが挙げられます。
最適レギュレータの考え方
次に、最適レギュレーター問題でどういうことを考えていくかについて説明します。

最適レギュレーター問題では、まず次のような評価関数を考えます。

この評価関数は状態 xにQをかけた二次形式のものになっており、それと Ru に関する二次形式の項の線形和で表されています。評価区間は時刻 t = 0 から時刻無限大までとなっています。無限区間の評価区間です。
この評価関数値Jを最小にするようなゲインKを求める問題のことを最適レギュレーター問題と呼びます。ここで評価区間は時刻0秒を基準として無限大までとっていますが、ここは便宜上ゼロとしているだけで別の時刻からスタートしても構いません。
この二次形式の係数行列Qと Rは、重み行列と呼ばれるもので x を重視する場合にはQを大きめに取る、入力uを重視する場合は Rを大きく取るといった扱いがなされます。第一項が小さければ小さいほど、x が早くゼロに収束するような解が良いことを意味しており、他方、第二項が小さいほど入力エネルギーが小さくて済む、ような解が良いということを意味しています。
そして最適レギュレーター問題では、この収束の速さとエネルギーの少なさを両立する
制御手法といえます。

最適レギュレータ問題の解
ここで最適レギュレーター問題の解を先に説明します。この最適レギュレーター問題の解は、すでに求められており以下のようなステップで求めることができます。

まずは図のステップ 1 で示すように、リカッチ方程式(リッカチ方程式, Liccati方程式)と呼ばれるこのこちらの方程式を満足する正定行列 Pを求めます。これが最初のステップです。
この解は、代数計算として求めることができます。
そして、ステップ 2 でこの得られた正解 Pを使って、ゲインを Rの逆行列かけるBの転置かけるPというふうに設定してやると、それが先ほどの最適レギュレーター問題に対する最適解になります。
下記ページで数値例を含めて詳細をまとめています。
状態オブザーバと併合系による制御
状態フィードバック制御では、全ての状態量(状態ベクトルの要素)が計測できる場合に利用できます。他方、出力数が状態数より少ない場合は、オブザーバを組むことにより出力フィードバック制御系としてシステムを構成することになります。
状態オブザーバの基本的な考え方
ここでオブザーバーの基本的な考え方について説明します。
まず制御対象のダイナミクスが以下の図の上部ように与えられていたとき、これに対して同じA, B, C 行列で与えられる、制御対象のコピーを計算機上に作成します。これを数理モデルと呼びます。制御対象に制御入力を印加したとき、それに対して出力が現れますが、制御対象と同じ入力を制御対象のコピーに印加してやると、数理モデルの状態は制御対象の状態に似た振る舞いをします。

仮に、システムのA行列の極が安定極の場合、さらに、制御対象の状態と数理モデルの状態の初期値が一致していれば、外乱なし環境下では制御対象の状態と数理モデルの状態とが全ての時刻で完全に一致します。
状態の初期値が一致していなくても、Aが安定な場合に関しては、この初期値の影響は時間の経過とともに小さくなっていきますので、入力を入れてしばらくすると制御対象の状態と制御対象のコピーである数理モデルの状態とが近くなっていきます。
このため、数理モデルの状態を制御対象の状態とみなして状態フィードバック制御で用いることができます。
ここでさらに、この制御対象の出力と、この制御対象のコピーにおける出力との偏差をフィードバックに用いることによってより収束の精度を良くすることができます(下図参照)。

以上がオブザーバーの考え方になります。
オブザーバの立式
具体的に基本となる状態オブザーバーは以下の式で与えられます。
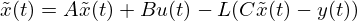
ここで、y(t)は観測出力です。
このような構成を行うことによって、状態の推定誤差は以下の図で示されるダイナミクスとなります。ここで A - LC の項が安定となるようにLを設定してやると、それによってeはゼロに漸近していきます。このオブザーバはAが不安定であっても(C,A)の組が可観測であれば実装可能です。
状態オブザーバについては以下でまとめています。
実機実験とシミュレーション
倒立振子の状態フィードバックによる安定化制御
MATLABシミュレーション
MATLABシミュレーションについては、次のページでまとめています。
状態空間モデルの応用(Mamba)
ネットワークアーキテクチャとしてTransformerを凌駕しうるモデルとして提案されているMambaでは、制御で利用する状態空間モデルが用いられています。詳しい内容は以下で解説されています。
【Mamba】Transformerを凌駕しうるアーキテクチャを徹底解説(ソースコードあり) #Python - Qiita
Mamba解析:AIシーケンスモデリングの新時代への挑戦 | Reinforz Insight
Mamba: Linear-Time Sequence Modeling with Selective State Spaces (Paper Explained) - YouTube
制御工学チャンネル内の状態フィードバック制御関連ページ
動画ポータルサイト「制御工学チャンネル」内の状態方程式に基づいた制御へのリンクはこちらです。各教員ごとのページとしてまとまっています。
状態方程式に基づく制御
自己紹介
岡島 寛 (熊本大学工学部情報電気工学科准教授)
制御工学の研究をしています。モデル誤差抑制補償器,状態推定,量子化制御など
研究室HP
岡島寛 (システム制御 control-theory.com)
English Web Page
Hiroshi Okajima (Control Engineering control-theory.com)
制御動画ポータルサイト
制御工学チャンネル(伝達関数・状態方程式・MATLABなど)
電気動画ポータルサイト
以上が状態フィードバック制御の記事全体をまとめた記事になります。本記事は以上です。役に立った、と思われましたら、ブックマーク・シェア等のアクションをしていただければ嬉しいです。