状態方程式表現されたシステムの安定性
この記事では状態方程式表現されたシステムの安定性についてまとめます。安定性に関する動画は最下部に置いています。なお、状態方程式に基づく制御・状態フィードバック制御の全体像は次の記事でまとめています。
制御対象の極と安定性
ここでは、制御系の安定性について説明したいと思います。まずは、以下のシステムが与えられているものとします。
\begin{equation} \dot x(t) = Ax(t) + Bu(t) \\ y(t) = Cx(t) \end{equation}
各種パラメータの特徴は状態方程式の基礎としてまとめています。
このとき、与えられたシステムが安定か否かはの特徴を調べればよく、特に行列
の固有値によって特徴付けられます。
行列は正方行列であり、以下の式を解くことにより固有値を求めることができます。
\begin{equation} det ( A-\lambda I) = 0\end{equation}
ここで、は単位行列です。
が
の行列の場合、固有値は
個存在します。
この固有値を確認し、全ての固有値の実部が負であれば、システムは漸近安定です。
他方、固有値の実部に正または零が含まれている場合には、システムは不安定もしくは安定限界となります。
ここでは、システムの次数の場合と、次数
の場合のそれぞれで安定性について確認します。
制御対象の次数が1の場合
ここでは、状態数1のスカラシステムを考えます。は行列ではなくスカラ値です。
のとき、状態方程式は次のように書けます。
\begin{equation} \dot x(t) = -x(t) + u(t)\end{equation}
この状態方程式の解は
となり、であれば、初期状態
によらず
は時間の経過と共に零に漸近します。他方、
とすると
となり、発散します。仮に、のとき、状態方程式は
\begin{equation} \dot x(t) = u(t) \end{equation}
であり、これは、入力の積分値が状態
となることを意味します。例えば、
がステップ信号の場合、状態
は発散します。
制御対象の次数が3の場合
次の行列が与えられている場合を考えます。
\begin{equation} A = \begin{bmatrix} -1 & 0 & 0\\0 &-2&0\\0&0&-3\end{bmatrix}\end{equation}
このとき、固有値はであり、全ての固有値の実部が負ですので漸近安定となります。制御系を解析する場合、固有値を複素平面でプロットします。この例について固有値を複素平面にプロットすると次図のようになります。
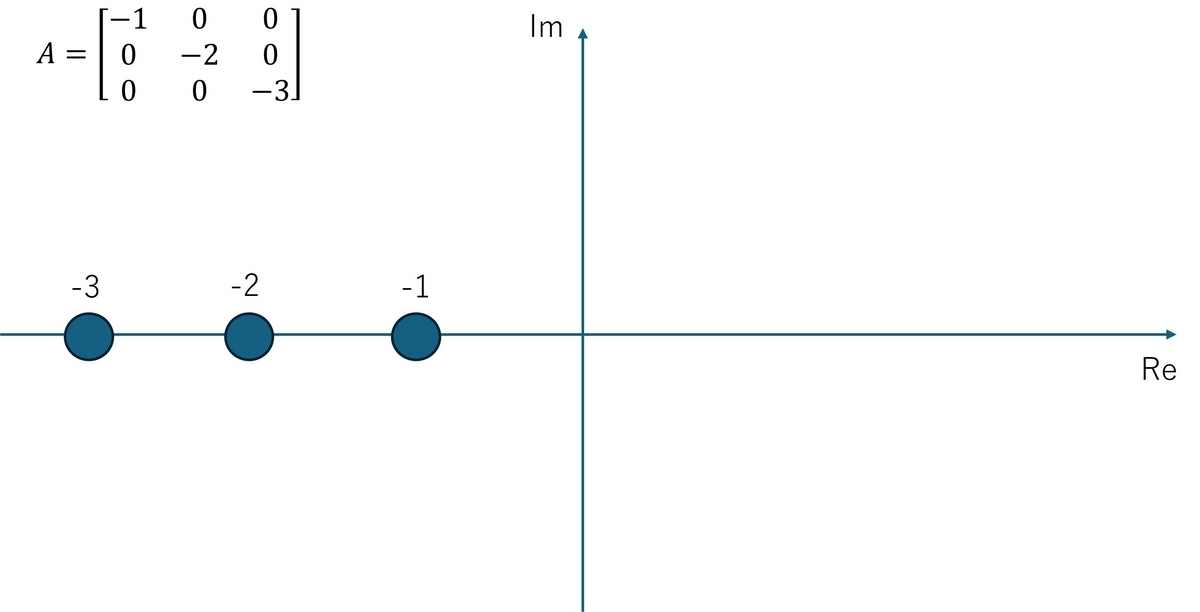
行列の固有値01
次に、が次式で与えられる場合を考えます。
\begin{equation} A = \begin{bmatrix} -1 & 0 & 0\\0 &-2&-1\\0&1&-2\end{bmatrix}\end{equation}
このとき、固有値はであり、全ての固有値の実部が負ですので前のものと同様に漸近安定となります。この例について固有値を複素平面にプロットすると次図のようになります。
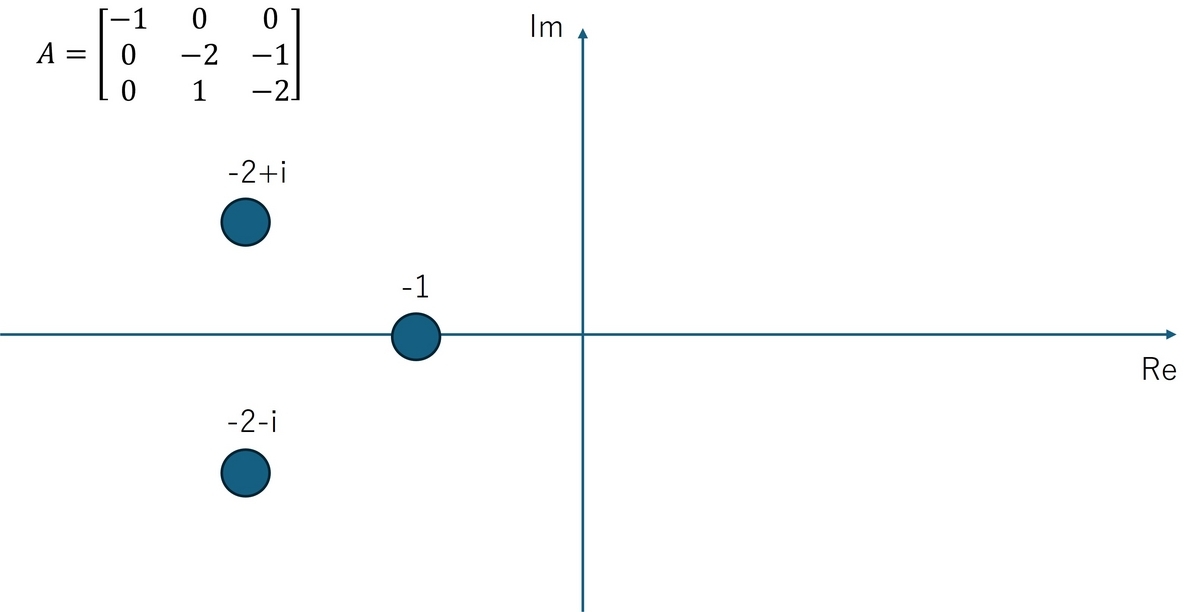
行列の固有値02
最後に、が次式で与えられる場合を考えます。
\begin{equation} A = \begin{bmatrix} -1 & 0 & 0\\0 &1&-1\\0&1&1\end{bmatrix}\end{equation}
このとき、固有値はであり、実部が正の固有値を含むため不安定となります。この例について固有値を複素平面にプロットすると次図のようになります。
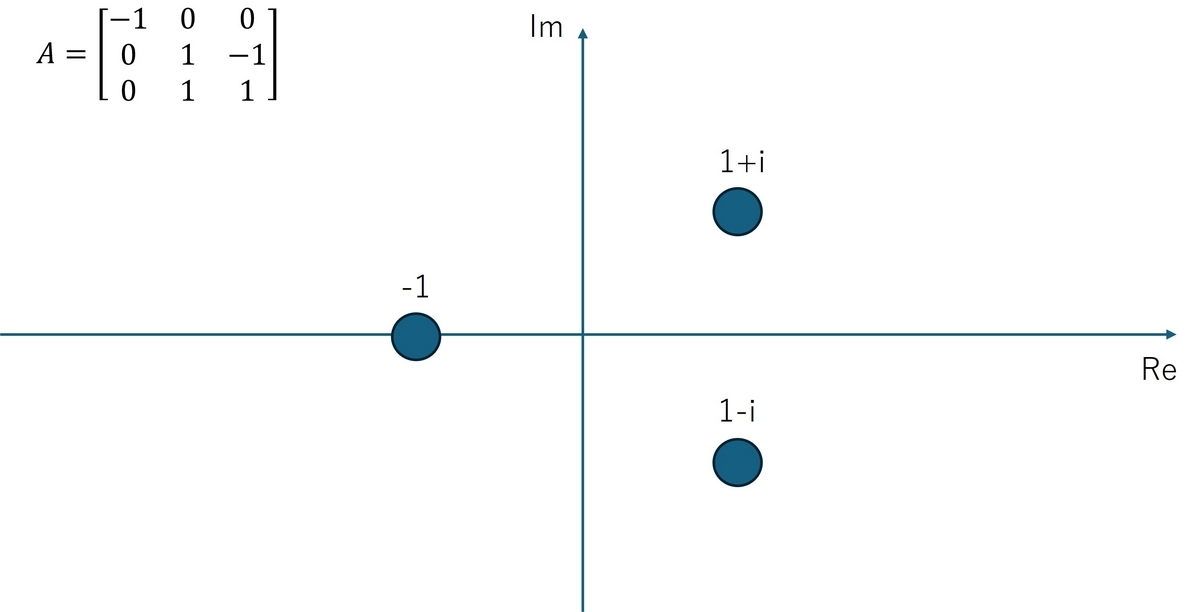
行列の固有値03
安定性だけでなくその応答の特徴をみながら設計がされます。極配置については以下の記事で説明しています。
リアプノフの安定判別法
それでは次にリアプノフの安定判別法について説明していきます。リアプノフの安定判別法は自律システムの安定性を解を求めることなく判別する有力な安定性判別手法になります。
非線形システムに対応できるなど、かなり有力なツールとなっています。基本的なアイディアは以下の通りです。
まずスカラ値関数を考えます。これは任意の
に対して常に正値をとる正定値関数です。例えば、例えば
\begin{equation} V(x)=x^T P x\end{equation}
としてを正定行列と設定してやるとこれは正定値関数となります。
このとき、の時間微分が常に負であれば
の値は時間の経過とともに常に減少していくことになります。これがリアプノフ関数を利用した安定性判別の基本的なアイディアになります。
線形システムに対するリアプノフ方程式
線形システム(自律系)に対してリアプノフ方程式は自律系の行列および行列
から構成される以下の式です。
\begin{equation} A^T P+ P A + Q =0\end{equation}
この式を満たすような正定行列および半正定行列
の組が存在すれば、システムは漸近安定となります。もし、
の固有値の実部が全て負の場合は、適当に与えた
に対して、リアプノフ方程式を解き、得られた
が正定行列となることが知られています。このとき、リアプノフ関数は
\begin{equation} V = x(t)^T P x(t)\end{equation}
と与えられ、その微分値は
であり、さらに、リアプノフ方程式を満足するは半正定であり
\begin{equation}\dot V = - x(t)^T Q x(t)\end{equation}
としてが常に非正となり単調減少します。
MATLABで安定性解析をするプログラム例を示します。
A = [-1 0 0;0 -2 -1;0 1 -2];
Q = [1 0 0;0 1 0;0 0 1]; %単位行列
P = lyap(A,Q);
このとき、出力結果は次のようになります。
P = 0.5000 0 0
0 0.2500 0
0 0 0.2500
実際、得られたを用いて
を計算すると0になります。また、当然のように
は正定行列となっています。
なお、不安定システムに対して上記の関数lyapを適用しても正定となるようなは求まりません。
MATLABライブスクリプトファイル
次のリンクにMATLABライブスクリプトファイルを置いています。これは、リアプノフの安定判別法の動画でも詳しく説明しています。
安定性に関する動画
以下は,状態方程式表現されたシステムの極と安定性について説明した動画になります。
以下は,状態方程式表現されたシステムのリアプノフの方法について説明した動画になります。
関連記事
自己紹介
岡島 寛 (熊本大学工学部情報電気工学科准教授)
制御工学の研究をしています。モデル誤差抑制補償器,状態推定,量子化制御など
研究室HP
岡島研究室(システム制御 control-theory.com)
制御動画ポータルサイト
制御工学チャンネル(伝達関数・状態方程式・MATLABなど)
電気動画ポータルサイト
本記事をお読みいただきありがとうございます。役に立った、と思われましたら、ブックマーク・シェア等のアクションをしていただければ嬉しいです。

